BRAINBOARD

Ein guter Start sich mit der logistischen Regression zu beschäftigen, ist (James et al. 2013), pp 127-138. Hier werden zahlreiche Möglichkeiten zur Nutzung und für Variationen der logistischen Regression dargestellt. In dieser Arbeit soll auf Basis eines echten Datensatzes (vgl.(Nikhil, n.d.)) die Techniken der logistischen Regression mit Hilfe der statistischen Programmiersprache R dargestellt und dabei zudem verschiedene Optimierungsmöglichkeiten aufgezeigt werden.

I. Die logistische Regression

Ausgangspunkt einer logistischen Regression sind die quantitativen und qualitativen Ausprägungen (=Prädiktoren) $X_i$, $i=1, \dots, k$ unterschiedlicher Kreditnehmer. Dabei wird eine qualitative Ausprägung mit $m$ Ausprägungskategorien (z.B. verheiratet, ledig, geschieden) auf die Zahlen $0, \dots, m$ kodiert. Ziel der logistischen Regression ist es, anhand der Ausprägungen $X_i$ die Wahrscheinlichkeit für einen Ausfall $Y=1$ unter der Bedingung der einzelnen Prädiktoren $X_i$ $$P\left(Y=1\left|\left(X_i\right)_{i=1, \dots, k}\right.\right)$$ für neue Kredite/Kreditnehmer zu schätzen.

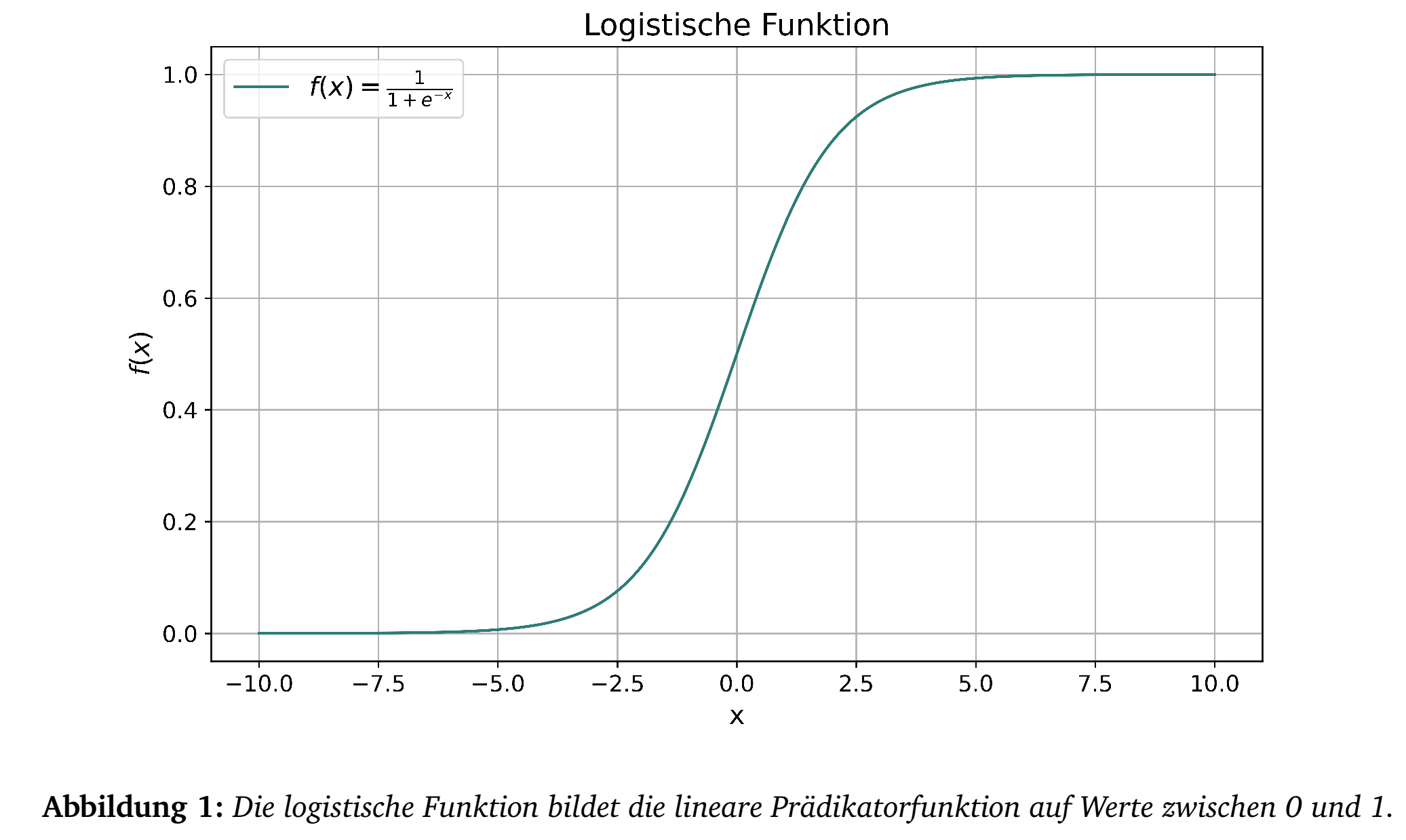
In der logistsichen Regression sind die Ausfallwahrscheinlichkeiten von einer linearen Gewichtung der Prädikatoren $X_i$ abhängig, d.h. von einem Wert $$Z(X) =\beta_0 + \beta_1 X_1 + \dots \beta_k X_k.$$ $Z(X)$ heißt lineare Prädikatorfunktion. Durch Anwenden der logistischen Funktion $$\frac{e^{Z(X)}}{1+e^{Z(X)}} = \frac{1}{1+e^{-Z(X)}}$$ wird $Z(X)$ auf einen Wert zwischen $0$ und $1$ abgebildet und kann so als Wahrscheinlichkeit interpretiert werden (vgl. Abbildung 1).

Ziel der logistischen Regression ist es, mittels Stichproben aus der Vergangenheit $\beta_0, \dots, \beta_k$ so zu ermitteln, dass $$p(X) = \frac{e^{\beta_0 + \beta_1 X_1 + \dots \beta_k X_k}}{1+e^{\beta_0 + \beta_1 X_1 + \dots \beta_k X_k}}$$ ein möglichst guter Schätzer für $$P\left(Y=1\left|\left(X_i\right)_{i=1, \dots, k}\right.\right)$$ ist. Hierzu wird die Maximum Likelihood Methode benutzt, d.h. hat man $n$ Stichproben der Ausprägungen $x^{(j)}_i$, $i=1, \dots, k$ für $j=1, \dots n$ Kreditnehmer und definiert man $y^{(j)} = 1$ falls der Kreditnehmer $j$ in der Vergangeheit ausgefallen ist und $y^{(j)} = 0$ sonst, dann muss folgende Funktion in Abhängigkeit von $\beta_0, \dots, \beta_k$ maximiert werden: $$\begin{equation} \max_{\beta_0, \dots, \beta_k} \mathcal{L}(\beta_0, \dots, \beta_k) = \prod_{j:y^{(j)}=1} p(x^{(j)}) \cdot \prod_{j:y^{(j)}=0} \left(1-p(x^{(j)})\right), \end{equation}$$ dabei ist $x^{(j)}= (x_1^{(j)}, \dots, x_k^{(j)})$.

Zur Maximierung von (1) gibt es verschiedene mathematische Verfahren. Am üblichsten ist das Fisher-Scoring-Verfahren^f1 (vgl. (Fahrmeir, Kneib, and Lang 2009), pp 198-201 und p202). Diese Lösungsmethode ist auch in der Programmiersprache R umgesetzt.

II. Vorbereitung der Daten

Im Folgenden wird beispielhaft die Regression auf Basis des frei verfügbaren Datensample von (Nikhil, n.d.) durchgeführt. Nachdem der Originaldatensatz über 255.000 Datensätze beinhaltet und nur demonstrativ die Funktion der logistischen Regression dargestellt werden soll, werden hieraus 5000 Datensätze zufällig ausgewählt. 3000 der Datensätze (als Mappe "Input" in Excel) dienen als Input für die Regression, auf Basis der anderen 2000 Datensätze (als Mappe "Test") soll das Modell getestet werden. Die Kategorie-Prädiktoren wurden im Excel mit den Werten 1 und aufsteigend bzw. $0$ und $1$ (für No/Yes) überschrieben.

Die Daten werden zudem über die Min-Max-Normierung auf Werte zwischen 0 und 1 normiert. Ziel ist es, die Daten so zu transformieren, dass sie eine gemeinsame Skala haben, ohne dabei die Unterschiede in den Bereichen der Werte zu verzerren. Dabei wird für jede Reihe der Input-Daten (d.h. für jeden Prädikator $x_i$) das Maximum und das Minimum bestimmt und die Daten in der Input-Mappe als auch in der Test-Mappe normiert^f2. Die neuen Daten haben dann die Form $$x^{(j)}_{i,\text{norm}} = \frac{x^{(j)}_{i}-\min^{\text{input}}_j(x_i^{j})}{\max^{\text{input}}_j(x_i^{j})-\min^{\text{input}}_j(x_i^{j})} \text{ für alle } j=1, \dots, n_{\text{Input}} \text{ bzw. }n_{\text{Test}}\text{ und } i=1, \dots, k.$$ Hat man mit Hilfe der logistischen Regression $\beta$-Werte für die normierten Daten gefunden, so kann man diese folgendermaßen auf die Ursprungsdaten anpassen: $$\begin{equation} \beta_{i}^{original} = \beta_{i}^{norm} \cdot \frac{1}{\max^{\text{input}}_j(x_i^{j})-\min^{\text{input}}_j(x_i^{j})} \end{equation}$$ und $$\begin{equation} \beta_{0}^{original} = \beta_{0}^{norm} - \sum_{i=1}^{k} \left( \beta_{i}^{norm} \cdot \frac{\min^{\text{input}}_j(x_i^{j})}{\max^{\text{input}}_j(x_i^{j})-\min^{\text{input}}_j(x_i^{j})} \right). \end{equation}$$ Alle Datenvorbereitungen lassen sich auch direkt über R durchführen. Zur Übersichtlichkeit sind jedoch alle beschriebenen vorbereiteten Maßnahmen in einem Excel-Sheet ’"Test_log.xlsx’" mit den Mappen "Input" und "Test".

Wie bei allen Datenanalysen sollten Datensätze, die unplausible Werte zeigen, im Vorfeld und vor weiteren Datenbearbeitungen (z.B. Normierung etc.) entfernt werden. Extreme Ausreißer in einzelnen Parametern sollten entweder auf 2 Standardabweichungen beschränkt oder der entsprechende Datensatz überarbeitet bzw. entfernt werden.

III. Logistische Regression in R

Zunächst werden die vorbereiteten Daten aus dem Excel-File in R eingelesen.

# Logistische Regression mit R
# Erstellung: 05.04.2024
# install.packages("openxlsx") # falls noch nicht installiert
library(openxlsx) 
setwd("C:/Daten") # setzt den Pfad der Daten
Input=read.xlsx("Test_log.xlsx", sheet = "Input") # Liest die Daten aus Mappe Input
summary(Input) # Zusammenfassung der Input-Daten

Der Befehl summary(Input) gibt eine Zusammenfassung der Input-Datei mit Angabe einiger Verteilungsparameter der einzelnen Prädikatoren. Die letzte Spalte heißt Default. Hier ist mit 0 "kein Ausfall" und 1 "Ausfall" der Zielvektor definiert. Mean zeigt dabei die mittlere Ausfallrate der Input-Dateien.Im nächsten Schritt wird die logistische Regression durchgeführt:

Modell_1 = glm(Default ~ ., data = Input, family = binomial) # Regression
summary(Modell_1) # Zusammenfassung Modell 1
coef_M1 = as.data.frame(Modell_1$coefficients) # speichere die Koeffizienten von Modell 1
write.xlsx(coef_M1, "coef_M1.xlsx", rowNames = TRUE) # schreibe die Koeffizienten von Modell 1 in Excel

glm ist der Funktionsaufruf für die allgemeinen linearen Modelle. family = binomial gibt an, dass ein binäres Modell oder logistisches Modell zur Anwendung kommt. Default ist die Zielvariable und über $\sim$ . werden alle verfügabren Prädikatoren für die Regression eingesetzt. Mit Default $\sim$ Income + DTIRatio würden entsprechend nur diese beiden Prädikatoren in die Rechnung einbezogen.

Die summary des Modells (vgl. Abbildung 2) gibt zu jedem $\beta$-Faktor den geschätzten Wert, die geschätzte Standardabweichung, den hieraus berechneten Z-Wert einer Normalverteilung und den P-Wert des Z-Wertes. Die *-Bezeichnung gibt die Signifikanz an, d.h. je kleiner der P-Wert^f3, umso höher die Signifikanz des $\beta$-Faktors und desto mehr Anzahl von *.

Der Dispersionsparameter von 1 gibt an, dass die Varianz der $\beta$-Faktoren aus der Streuung der Mittelwerte berechnet wurde (dies ist Standard für family = binomial).

Die Null deviance bei den angegebenen Freiheitsgraden zeigt an, wie ein Modell ohne Prädikatoren abschneiden würde (d.h. nur mit $\beta_0$) und kann mit einer $\chi^2$-Verteilung mit den entsprechenden Freiheitsgraden vergleichen werden. Die Residual deviance gibt das entsprechende für das volle Modell an. Ein perfektes Modell hätte die Deviance von $0$, d.h. je niedriger desto besser.

Der AIC ist ähnlich zur Deviance ein Maß für die Qualität des Modells. Es berücksichtigt zudem die Anzahl der verwendeten Parameter. Es ist $$\text{AIC}=k - 2 \ln (\mathcal{L}),$$ d.h. ist die gefundene Maximum-Likelihood $\mathcal{L}$^f4 sehr klein ($\ll 1$), dann wird $-2 \ln(\mathcal{L})$ sehr groß und damit entsprechend der AIC, oder anders: hat man zwei Modelle, dann nimmt man das Modell mit dem kleineren AIC.

Die Koeffzienten $\beta_0, \dots, \beta_k$ werden in ein Excel-File abgespeichert und können über (2) und (3) in $\beta$-Werte der ursprünglichen, nicht-normierten Daten überführt werden.

IV. Testen der logistischen Regression

Um die Qualität der gefundenen Regression zu Testen, werden die Test-Daten in R hochgeladen. Die tatsächlichen Werte für Default werden dabei mit den prognostizierten Werten verglichen:

Test=read.xlsx("Test_log.xlsx", sheet = "Test") # Liest die Daten aus Mappe Test
vorhersagen = predict(Modell_1, newdata = Test, type = "response") # berechnet die Ausfallwahrscheinlichkeiten aus dem Modell 1
vorhersagen_binaer = ifelse(vorhersagen > 0.2, 1, 0) # definiert, ab welcher Ausfallwahrscheinlichkeit der Kreditnehmer als ausgefallen gilt
table(Tatsaechliche = Test$Default, Vorhersagen = vorhersagen_binaer) # Confusion Matrix 

predict(Modell_1, newdata = Test, type = "response") berechnet auf Basis der geschätzten $\beta$ aus Modell 1 und den Testdaten mit type = "response" die jeweiligen geschätzten Ausfallwahrscheinlichkeiten.

In vorhersagen_binaer werden diese Ausfallwahrscheinlichkeiten dann einem Ausfall (1) (=Positive) oder Nicht-Ausfall (0) (Negative) zugeordnet, je nachdem ob die (frei wählbare) Ausfallgrenze $0.2$^f5 überschritten wurde.

Je höher die Schwelle, desto weniger Ausfälle werden prognostiziert, d.h. P(Vorhersage kein Ausfall| Ausfall tritt ein) nimmt zu. Wenn die Nullhypothese

gilt, dann entspricht das dem $\alpha$-Fehler (=FP), der daher mit steigendem Schwellenwert zunimmt. Gleichzeitig nimmt der $\beta$-Fehler P(Vorhersage Ausfall|Ausfall tritt nicht ein) (=FN) zu^f6.

Der Code in der letzten Zeile gibt eine Confusion Matrix aus. Diese fasst die Ergebnisse in True Negative (TN), False Positive (FP) (1. Zeile), False Negative (FN) und True Positive (TP) (2. Zeile) zusammen.

Eine wichtige Größe zur Beurteilung der Qualität des Modells ist die RO . Hier werden die Ausfallraten der Testdaten absteigend sortiert und jeweils die Anzahl der Ausfälle, die im Bereich darunter liegen (=$\alpha$) und die Nichtausfälle die im Bereich darüber liegen (=$\beta$) gezählt , jeweils normiert mit den gesamten Ausfällen bzw. gesamten Nicht-Ausfällen. Jeder Schuldner bekommt so einen $(\beta,1-\alpha)$-Punkt. Die daraus entstehende ROC. Die Fläche darunter heißt AUC. Die AUC misst die Qualität der aus der Regression ermittelten Ausfallwahrscheinlichkeiten. Es ist Gini = 2 AUC - 1.

#install.packages("pROC") # falls noch nicht installiert
library(pROC) # laedt das ROC-Paket
roc_objekt = roc(Test$Default, vorhersagen) #ROC auf Basis der Testdaten
plot(roc_objekt, main="ROC Kurve") # Plot der ROC-Kurve
auc(roc_objekt) # Berechnung der AUC

Nachdem der Intercept $\beta_0$ eine Konstante ist und mit der gleichen Höhe auf alle Prognosen wirkt, hat eine Veränderung von $\beta_0$ keine Auswirkung auf die ROC bzw. den AUC (die Reihung bleibt bei Veränderung von $\beta_0$ gleich). $\beta_0$ kann daher als Kalibrierung für die erzeugten Ausfallwahrscheinlichkeiten benutzt werden. Ein höheres $\beta_0$ erzeugt höhere Ausfallraten und vice-versa wie Abbildung 1 zeigt. $\beta_0$ geht hier linear in den x-Wert der logit-Funktion ein. In Abschnitt 7 wird dieser Effekt näher beschrieben und zur Kalibrierung der logistischen Regression benutzt.

V. Verbesserung 1: Auswahl der Prädikatoren

In der obigen Regression wurden alle verfügbaren Prädikatoren verwendet. Das muss nicht die beste Wahl sein. So kann das Model zu genau an die Inputdaten angepasst sein und die Testdaten trotzdem ungenügend vorhersagen (Over-fitting). Zudem ist es oft leichter ein Modell mit weniger Prädikatoren zu interpretieren. Nachfolgend werden zwei Methoden zur Auswahl der Prädikatoren vorgestellt.

V.1 Subset Selection

Eine einfache Möglichkeit wäre, die Prädikatoren zu entfernen, die in der Auswertung einen hohen P-Wert aufweisen (summary(Modell_1) in Abbildung 1). Ein hoher P-Wert ist ein Indiz, dass der entsprechende Prädikator nicht signifikant für das Modell ist. Das Modell_1 hat hier für die Prädikatoren DTIRatio, Education, MartialStatus und LoanPurpose einen P-Wert von größer 0.1. Der AIC des Modell_1 ist 1937.1. Die AUC auf den Testdaten 0.6771. Es wird ein zweites Modell aufgebaut ohne die erwähnten Prädikatoren:

Modell_2 = glm(Default ~ Age+Income+LoanAmount+MonthsEmployed+EmploymentType+HasMortgage+HasDependents, data = Input, family = binomial) # Regression
summary(Modell_2)
vorhersagen = predict(Modell_2, newdata = Test, type = "response")
roc_objekt = roc(Test$Default, vorhersagen)
auc(roc_objekt)

Der AIC von Modell_2 ist mit 1935.6 leicht besser. Die AUC mit 0.6774 fast unverändert. In Summe hat sich das Modell - trotz Reduktion der Prädikatoren von 11 auf 7 - leicht verbessert.

Es gibt verschiedene Heuristiken die Auswahl der Prädikatoren zu verbessern. Eine Übersicht hierzu gibt (James et al. 2013), 6.1 Subset Selection, pp 205-214. Im Wesentlichen werden hier über Algorithmen die Prädikatoren systematisch hinzugefügt oder entfernt, je nachdem ob sich der AIC dadurch verbessert. Auch in R gibt es einen Best-Subset-Algorithmus:

#install.packages("glmulti") # falls noch nicht installiert
library(glmulti) # laedt das Best Selection
Modell_3=glmulti(Default ~ ., data = Input, 
family = binomial, 
method = "g",
level = 1,   
fitfunction = "glm")
Modell_3@objects[[1]] # gibt die optimalen Praedikatoren und den AIC aus
vorhersagen = predict(Modell_3@objects[[1]], newdata = Test, type = "response")
roc_objekt = roc(Test$Default, vorhersagen)
auc(roc_objekt)

glmulti führt zahlreiche Regressionen mit wechselnden Prädikatoren aus. Dabei wird stets der AIC berechnet. Die Prädikatoren, die das kleinste AIC erzeugen, werden abschließend ausgewählt. Sind viele Prädikatoren zu Beginn vorhanden, ist der Algorithmus sehr rechenintensiv. Für method= gibt es folgende Optionen (vgl. (James et al. 2013), Abschnitt 6.1):

• h (Exhaustive): Eine vollständige Suche, bei der alle möglichen Kombinationen der angegebenen Prädiktoren berücksichtigt werden. Diese Methode ist sehr gründlich, kann aber extrem rechenintensiv und langsam sein, besonders bei einer großen Anzahl von Prädiktoren. ACHTUNG: Es werden hier $2^k$ Regressionen durchgeführt, wobei $k$ die Anzahl der auszuwählenden Prädikatoren ist, d.h. bei $k=10$ sind das schon 1024 durchzurechnende Regressionen. Bei größeren Werten von $k$ ist diese Methode nicht mehr praktikabel.
  

• g (Genetic): Eine genetische Suche, die genetische Algorithmen verwendet, um effizient durch den Raum der möglichen Modelle zu navigieren. Genetische Algorithmen simulieren den natürlichen Evolutionsprozess, um optimale Lösungen zu finden, und sind in der Regel schneller als die exhaustive Suche, besonders bei großen Datensätzen.
  

• f (Forward): Eine sequenzielle Vorgehensweise, bei der mit dem leeren Modell begonnen wird und schrittweise Variablen hinzugefügt werden, die die Modellgüte am meisten verbessern.
  

• b (Backward): Eine weitere sequenzielle Methode, die mit dem vollständigen Modell beginnt, bei dem alle Variablen einbezogen sind, und schrittweise jene Variablen entfernt, die die geringste Verbesserung der Modellgüte bieten.
  

• l (Leap): Eine Mischung aus Forward- und Backward-Methoden, oft als "Stepwise Regression" bezeichnet, bei der sowohl Variablen hinzugefügt als auch entfernt werden können.
  

Über Level lassen sich auch komplexere Kombinationen der Prädikatoren mit einbeziehen. Für Level=1 werden die Prädikatoren an sich betrachtet. Für Level=2 werden auch Produkte von je zwei Prädikatoren in die Optimierung einbezogen und bei Level=3 auch Produkte höherer Ordnung zugelassen. Höhere Levels können die Daten im Allgemeinen besser beschreiben, es besteht aber die Gefahr des Over-Fittings der Input-Daten. Zudem ist die Interpretation von Produktprädikatoren meist nicht intuitiv.

Nach Abruf des Skripts oben wurden aus allen verfügbaren Prädikatoren die Prädikatoren Education und MartialStatus entfernt. AIC und AUC haben sich mit 1934 bzw. 0.6784 leicht verbessert.

V.2 Lasso-Methode

Auch die Lasso-Methode verfolgt das Ziel, Prädikatoren aus der Regression zu nehmen, die für eine Prognose unwichtig sind (vgl. (James et al. 2013), 6.2.2, pp 219-228). Hierzu wird die Gleichung (1) um einen Regulationsterm ergänzt, d.h. die neue zu maximierende Funktion ist $$\begin{equation} \max_{\beta_0, \dots, \beta_k} \mathcal{L}(\beta_0, \dots, \beta_k) = \prod_{j:y^{(j)}=1} p(x^{(j)}) \cdot \prod_{j:y^{(j)}=0} \left(1-p(x^{(j)})\right) - \lambda \sum_{i=1}^k |\beta_k|. \end{equation}$$ Dabei ist $\lambda > 0$ ein zu wählender Regulationsterm. Ist $\lambda$ groß, dann wird das Maximum gefunden, bei dem die $\beta_j$ fast überall $0$ sind. Ist $\lambda$ sehr klein, spielt der zu (1) ergänzte Term beim Finden eines Maximums nahezu keine Rolle. Die Wahl des passenden $\lambda$ ist somit entscheidend.

Ähnlich zu den Ausführungen in Abschnitt 5.1 werden auch hier verschiedene Lambdas ausprobiert. Bei jedem Lambda wird eine K-fache Kreuzvalidierung durchgeführt. Dabei werden die Trainingsdaten in K Subdaten aufgeteilt (K ist im Allgemeinen 10). Anschließend werden 10 Regressionen durchgeführt, wobei jeweils K-1 Subdatenpools als Training und 1 Subdatenpool als Validierungsdatensatz benutzt wird. Für jeden Validerungsdatensatz wird jeweils die Devianz berechnet und diese über die K Läufe gemittelt. So erhält man für jedes $\lambda$ eine gemittelte Devianz. Dies wird automatisch von R gemacht und erfordert keinen Eingriff in die Daten.

Das Lambda mit der kleinsten Devianz heißt lambda.min. Die Standardabweichung von lambda.min auf Basis der $K$-Validierungen definiert einen Devianztoleranzbereich. Das größte $\lambda$, das in diesem Devianzbereich liegt, ist lambda.1se. Mit lambda.1se wird damit das sparsamste (weniger Prädikatoren) gewählt, dass immer noch eine akzeptable Leistung hat. Ein solches Modell ist im Allgemeinen robuster, d.h. nicht auf den Trainingsdaten "over-fitted".

Auch hier bietet R das entsprechende Werkzeug:

#install.packages("glmnet") # falls noch nicht installiert
library(glmnet) # laedt das Paket
x = as.matrix(Input[, -which(names(Input) == "Default")]) # als Input wird eine Matrix benoetigt
y=Input$Default # y ist der Zielwert - Spaltenname: Default
Prae=colnames(x) # Praedikatorennamen 
Modell_4p=cv.glmnet(x, y, family = "binomial", alpha = 1) # Lasso-Modell
coefficients_vector=as.vector(coef(Modell_4p, s = "lambda.1se")[-1]) # Koeffizienten der Regression mit lambda.1se. Hier sind einige 0.
aPrae=Prae[coefficients_vector != 0] # Auswahl der Koeffizienten != 0
formula = as.formula(paste("y ~", paste(aPrae, collapse = " + "))) # y ~ Koef1 + ... Koefk
Modell_4 = glm(formula, data = Input, family = binomial()) # logistische Regression
summary(Modell_4) # Zusammenfassung
vorhersagen = predict(Modell_4, newdata = Test, type = "response") 
roc_objekt = roc(Test$Default, vorhersagen)
auc(roc_objekt)

Zunächst werden  die Inputdaten in eine Datenmatrix transformiert. In der fünften Zeile werden die einzelnen Prädikatorennamen ausgelesen. Anschließend wird der Algorithmus zum Finden des besten $\lambda$ aufgerufen.

alpha=1 bedeutet, dass nur die L1-Norm $|\cdot|_1$ benutzt wird, bei kleinerem alpha wird mit der euklidischen L2-Norm gemischt. In Zeile 35 werden die Regressions-Koeffizienten für das Lambda lambda.1se ausgelesen. sPrae sind die Koeffizienten der Prädikatoren die nicht $0$ sind. Anschließend wird über formula aus diesen Koeffizienten die Regressionsgleichung erstellt und ausgewertet.

Das über die Lasso-Methode und den Beispieldaten erzeugte Modell hat aus den 11 ursprünglich vorhandenen Prädikatoren 5 entfernt. Die verbleibenden 6 Prädikatoren als logistische Regression haben ein AIC von 1937.9 und eine AUC auf den Testdaten von 0.677. Damit ist es nur unwesentlich schwächer als das Modell mit Einbezug aller Prädikatoren.

VI. Verbesserung 2: SMOTE - Balancing Inputdaten

Beim Finden einer sinnvollen logistischen Regression für Kreditausfälle gibt es oft das Problem der "unbalanced" Inputdaten, d.h. Ausfälle sind so selten, dass wesentlich mehr Daten für "Nicht-Ausfall" als "Ausfall" vorliegen. Betrachtet man Gleichung ([eq1]) $$\max_{\beta_0, \dots, \beta_k} \mathcal{L}(\beta_0, \dots, \beta_k) = \underbrace{\prod_{j:y^{(j)}=1} p(x^{(j)})}_{\text{Ausfälle}} \cdot \underbrace{\prod_{j:y^{(j)}=0} \left(1-p(x^{(j)})\right)}_{\text{Nicht Ausfälle}},$$ so sind die Faktoren des ersten Produkt meist viel weniger als die Faktoren des zweiten Produkts. Nachdem die Likelihood $\mathcal{L}$ hier nicht unterscheidet, spielen die Nicht-Ausfälle eine größere Rolle beim Auffinden des Maximums, d.h. die Regression legt ein höheres Gewicht auf die Nicht-Ausfälle.

Bei einem Kreditinstitut steht jedoch im Vordergrund, Ausfälle zu vermeiden⁷. Es wäre daher wünschenswert, ausgeglichene Daten für Ausfälle und Nicht-Ausfälle zu haben.

In der Praxis treten jedoch Ausfälle sehr selten auf. Man muss sich daher "synthetischen" Methoden bedienen, um dies zu erreichen. Eine dieser Methoden heißt SMOTE (= Synthetic Minority Over-sampling TEchnique) - vgl. (Chawla et al. 2002) bzw. (Mao, Lin, and Li 2013).

Die Klasse für die weniger Datensätze vorhanden sind (hier die Datenklasse mit Ausfällen) wird Minderheitenklasse genannt. SMOTE erzeugt synthetische Stichproben aus der Minderheitenklasse. Sie wird verwendet, um einen synthetisch ausgeglichenen oder nahezu ausgeglichenen Trainingsdatensatz zu erhalten, der dann verwendet wird, um die logistische Regression anzuwenden.

Die SMOTE-Stichproben sind lineare Kombinationen von zwei ähnlichen Stichproben aus der Minderheitenklasse. Zunächst wird dazu ein $x \in \mathbb{R}^k$ aus der Minderheitenklasse zufällig ausgewählt. Unter den K nächsten Nachbarn von $x$ in der Minderheitenklasse wird ein $x_R \in \mathbb{R}^k$ zufällig ausgewählt.⁸ Der neue synthetische Wert der Minderheitenklasse $x_S$ ist dann eine Linearkombination aus $x$ und $x_R$ $$x_S = x + t \cdot (x_R - x)$$ mit $t$ zufällig im Intervall $[0,1]$. Der Vorgang wird solange wiederholt, bis die Klassen ausgeglichen sind. Es wird meist $K=5$ gewählt.

Auch hier gibt es in R die entsprechenden Funktionen:

#01 SMOTE mit R
# Erstellung: 05.04.2024
# install.packages("openxlsx") # falls noch nicht installiert
library(openxlsx) 
setwd("C:/Daten") # setzt den Pfad der Daten
Input=read.xlsx("Test_log.xlsx", sheet = "Input") # Liest die Daten aus Mappe Input
# install.packages("smotefamily") # falls noch nicht installiert
library(smotefamily)
genData = SMOTE(Input[,-c(6,8,12)],Input[,12], K=5)$data 
names(genData)[names(genData) == "class"] = "Default" # umbennen der Spalte class aus SMOTE
genData$Default <- as.numeric(as.character(genData$Default)) # Default in nummerisches 0/1
wb = loadWorkbook("Test_log.xlsx") # Test-Sheet laden
if ("Input_S" %in% getSheetNames("Test_log.xlsx")) {removeWorksheet(wb, "Input_S")} 
addWorksheet(wb, "Input_S") # neues Input_S hinzufuegen
writeData(wb, "Input_S", genData)
saveWorkbook(wb, "Test_log.xlsx", overwrite = TRUE)

Obiger R-Code fügt dem ursprünglichen Excel-File eine neue Mappe mit den synthetischen ausgeglichenen Input-Daten hinzu (Mappe "Input_S"). Alle Modelle, die oben angegeben sind, können nun ebenso für diese Input-Mappe benutzt werden, indem Input durch Input_S beim Einlesen ersetzt wird, d.h. die Zeile 7 im Code auf Seite kann durch sheet = "Input_S" ersetzt werden.

Durch genData = SMOTE(Input[,-c(6,8,12)],Input[,12], K=5)$data werden die Spalten 6 und 8 aus den Inputdaten gestrichen, die bei Modell_2 als überflüssig gesehen wurden. Spalte 12 ist der Zielwert. SMOTE sollte auf das endgültige Modell, d.h. nach Entfernen der überflüssigen Prädikatoren angewandt werden, um sinnvolle synthetische Daten zu erzeugen.

Durch die Hinzunahme der synthetischen Daten hat sich das Modell bei Anwendung auf die Testdaten nur marginal auf AUC 0.6786 verbessert. Die SMOTE-Methode ist also also leider nicht immer erfolgreich. Allerdings gab es im vorliegenden Datensample bereits eine Ausfallrate von mehr als 10%. Bei Datensamples mit kleineren Ausfallraten sollte SMOTE erfolgreicher sein.

VII. Kalibrierung eines logistischen Modells

Die Funktion $$p(X) = \frac{e^{Z(X)}}{1+e^{Z(X)}}$$ mit $Z(X) =\beta_0 + \beta_1 X_1 + \dots \beta_k X_k$ kann als Ausfallwahrscheinlichkeit interpretiert werden. Allerdings ist $p(X)$ nur eine grobe Schätzung und in der Praxis kaum nützlich. Es gibt jedoch Möglichkeiten, $p(X)$ sinnvoll zu kalibrieren.

Nachdem $\beta_0$ von keinem Prädikator abhängig ist, ist für $\lambda=e^{\beta_0}$: $$p(X) = \frac{\lambda e^{Z_0(X)}}{1+\lambda e^{Z_0(X)}}$$ mit $Z_0(X) = \beta_1 X_1 + \dots \beta_k X_k$. Prinzipiell kann dieses $\lambda$ beliebig angepasst werden, ohne die Prognosefähigkeit (z.B. ROC und AUC) zu verändern. Es ist vielmehr eine Skalierung für die berechneten Ausfallwahrscheinlichkeiten $p(X)$ (vgl. Abbildung 3).

Meist ist es sinnvoll, $p(X)$ über $\lambda$ so zu kalibrieren, dass dies der durchschnittlichen Ausfallrate der letzten Jahre für ein solches Portfolio entspricht (=$\text{PD}_{TTC}$).

Durch einfache mathematische Verfahren (z.B. Newton) kann ein $\lambda^*$ gefunden werden, mit $$\frac{1}{m}\sum_{j:y^{(j)}=0} \frac{\lambda^* e^{Z_0(x^{(j)})}}{1+\lambda^* e^{Z_0(x^{(j)})}} = \text{PD}_{TTC},$$ dabei ist $m$ die Anzahl der nicht ausgefallenen Schuldner im Portfolio.

Auf diese Weise können den einzelnen Schuldnern interpretierbare Ausfallwahrscheinlichkeiten zugeordnet werden, ohne die AUC oder ROC der ursprünglichen logitischen Regression zu verändern. Zudem wird die erwartete Ausfallwahrscheinlichkeit $\text{PD}_{TTC}$ des Portfolios abgebildet.

Das gefunde $\lambda^*$ kann über $$\beta_0 = \ln(\lambda^*)$$ und Gleichung (3) dann in das Ratingsystem einfließen. Eine durchgeführte logistische Regression kann durch Veränderung des $\beta_0$ und damit des $\lambda$ so auf sinnvoll interpretierbare Ausfallwahrscheinlichkeiten kalibriert werden .

VIII. Credit Scores

Meist besteht eine Bonitätseinschätzung aus verschiedenen Teilen. So werden analytische Kennziffern verwendet (wie bei der logistischen Regression), aber zusätzlich auch weitere Score-Karten, die beispielsweise auf den Erfahrungen des Kreditanalysten beruhen.

Sinn des Scorings ist in erster Linie eine Reihenfolge der einzelnen Bonitäten zu finden und Grenzen zu definieren, ab welchem Score von einer Kreditvergabe abgesehen wird.

Für die endgültige Bonitätseinschätzung werden mehrere Scores gewichtet und zu einem Gesamtscore addiert, der das Rating des entsprechenden Kunden bestimmt. Als Bonitätsscore werden meist Zahlen von 0 bis 1000 benutzt, die beispielhaft folgende Informationen widerspiegeln:

800 - 1000 (Ausgezeichnet): Diese Kategorie repräsentiert die sichersten Kreditnehmer mit der geringsten Ausfallwahrscheinlichkeit. Kreditgeber bieten in der Regel die besten Konditionen, einschließlich niedriger Zinssätze und höherer Kreditlimits.

650 - 799 (Sehr gut): Kreditnehmer in dieser Kategorie gelten immer noch als risikoarm. Sie bekommen gute Kreditbedingungen, jedoch nicht ganz so vorteilhaft wie die Top-Kategorie.

500 - 649 (Gut): Diese Gruppe hat ein moderates Risiko. Die Konditionen sind weniger vorteilhaft, und es können höhere Zinsen anfallen.

350 - 499 (Ausreichend): Kreditnehmer hier haben ein erhöhtes Risiko, wodurch die Kreditbedingungen deutlich härter ausfallen. Höhere Zinssätze sind üblich.

150 - 349 (Schwach): Hochriskante Kreditnehmer, die oft nur unter strengen Bedingungen und zu sehr hohen Zinsen Kredite erhalten.

0 - 149 (Sehr schwach): In dieser Kategorie wird oft keine Kreditvergabe empfohlen, da das Ausfallrisiko sehr hoch ist.

Ordnet man den oben erwähnten Kategorien jeweils maximalen Ausfallwahrscheinlichkeiten zu, z.B. $0.1\%, 0.3\%, 1.5\%, 4\%, 8\%, 20\%, >20\%$, so kann man jeder Ausfallwahrscheinlichkeit und damit jedem Kunden aus der logistischen Regression über eine lineare Funktion einen Credit-Score zuordnen.

Hat man mehrere Scores kann auch die Gewichtung der einzelnen Scores für den Gesamtscore über eine Regression ermittelt werden. Auch hier läßt sich dann über ein entsprechendes $\lambda$ der Gesamtscore auf die erwartete Ausfallwahrscheinlichkeit kalibrieren.

Literatur

Chawla, Nitesh V., Kevin W. Bowyer, Lawrence O. Hall, and W. Philip Kegelmeyer. 2002.

“SMOTE: Synthetic Minority over-Sampling Technique.” Journal of Artificial Intelligence Research 16: 321–57.

Fahrmeir, Ludwig, Thomas Kneib, and Stefan Lang. 2009. Regression, 2. Auflage. Heidelberg: Springer.

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning. Springer.

Mao, BH, JC Lin, and YC Li. 2013. “SMOTE for High-Dimensional Class-Imbalanced Data.” BMC Bioinformatics 14 (1).

Nikhil. n.d. “Loan Default Prediction Dataset, 2022.” https://www.kaggle.com/datasets/nikhil1e9/loan-default.

Fußnoten