Der folgende Algorithmus beruht auf einer Promotionsarbeit. Leider ist die Originalarbeit von (Wegscheider 1993) nicht öffentlich verfügbar. Das hier dargestellte Vorgehen beruht daher auf der Beschreibung in (Schlittgen and Streitberg 1995). Zunächst sei hierzu eine Zeitreihe \(X=\{x_1, \cdots, x_n\}\), \(n\in \mathbb{N}\), vorgegeben. Die Menge \(T = \{1, \dots, n\}\) ist dabei die Indexmenge. \(X\) und \(T\) werden im Zeitablauf reduziert. Der Tupel \(P=(p_1, \dots, p_n)\) sind die Trendumkehrpotentiale der Werte in \(X\), d.h. der Wert \(x_i\) hat am Ende des Algorithmus das Trendumkehrpotential \(p_i\). Ziel ist es, nach und nach Punkte aus dieser Reihe zu löschen, die nur einen kleinen Beitrag zum "’großen"’ Trend beitragen. Dies geschieht in mehrern Schritten. Dabei bezeichnet \(X[j]\) bzw. \(T[j]\) das \(j\)-te Element in der Menge \(X\) bzw. \(T\). Nachdem im Algorithmus im Zeitverlauf Elemente aus \(T\) und \(X\) entfernt werden, ist nur zum Start \(X[j] = x_j\) bzw. \(T[j] = j\). \(\#T\) und \(\#X\) bezeichnen jeweils die Mächtigkeit von \(T\) und \(X\). Zu Beginn ist \(\#T = \#X=n\). Beide Größen werden im Algorithmus ständig durch Eliminierung von Punkten verkleinert.
I. Punkte ohne Trendumkehrpotential
Der erste Schritt ist, benachbarte Elemente mit gleichem Wert zu eliminieren. Anders als in (Schlittgen and Streitberg 1995) wird der Algorithmus in einem programmiernahen Code angegeben:

Nach Schritt 1 (vgl. Abbildung 1) wurde \(X\) und \(T\) um alle Elemente reduziert, deren
nachfolgender Nachbar den gleichen Wert hat. Die gelöschten Werte
spielen im Folgendem keine Rolle mehr. Aufgrund der Initialbelegung \(P=(0, \dots, 0)\) bleiben diese Werte bei
ihrem Trendumkehrpotential von \(0\).
II. Löschen von "’Minitrends"’
Es werden nun weiter Punkte aus \(X\) gesucht, die in einem "’Minitrend"’ von 3 Punkten in der Mitte liegen (vgl. Abbildung 2). Ein "’Minitrend"’ ist dabei eine Folge dreier aufsteigender oder dreier absteigender beiander liegender Werte der nach Schritt 1 verbleibenden Elemente aus \(X\).

Auch die nach Schritt 2
eliminierten Werte bleiben bei ihrem initialen Trendumkehrpotential von
0.
III. Sukzessive Berechnung der Trendumkehrpotentiale
Schritt 3 wird nun solange in einer Schleife durchlaufen, bis für jeden Punkt das Trendumkehrpotential gefunden wurde. Hierbei wird bei jedem Durchgang das \(i^* \in \{1, \dots , \#T - 1\}\) gesucht, bei dem die Differenz \(\left|X[i^*+1]-X[i^*]\right|\) unter allen verbleibenden Elementen in \(T\) minimal ist, d.h. \[i^{*} = \mathop{\mathrm{argmin}}_{i \in \{1, \dots , \#T - 1\}}\left\{\left|X[i+1]-X[i]\right|\right\}.\] Das entsprechende Element \(X[i^*]\) erhält dann das Potential \[p_{T[i^*]} = X[i^*+1]-X[i^*]\] und \(X[i^*+1]\) das Potential \[p_{T[i^*+1]}=-(X[i+1]-X[i]).\] Beide Werte werden anschließend aus \(T\) und \(X\) gelöscht. Ist einer der beiden Werte ein Randpunkt, dann wird das Potential nur für den Randpunkt gesetzt und nur dieser Wert gelöscht. Offensichtlich bleiben am Ende nach mehrmaligen Aufruf von Schritt \(3\) genau zwei Punkte übrig, die dann Randpunkte sind. Diese werden wie "’innere"’ Punkte behandelt. Der Algorithmus ist fertig.

Beispiel 1. In unterer Tabelle ist die Zeitreihe des EURUSD-Wechselkurses (Schlusskurs) vom 02.01.2023 bis zum 20.01.2023 angegeben. Die dazugehörigen Trendumkehrpotentiale \(p_i\) wurden mit obigen Algorithmus berechnet.
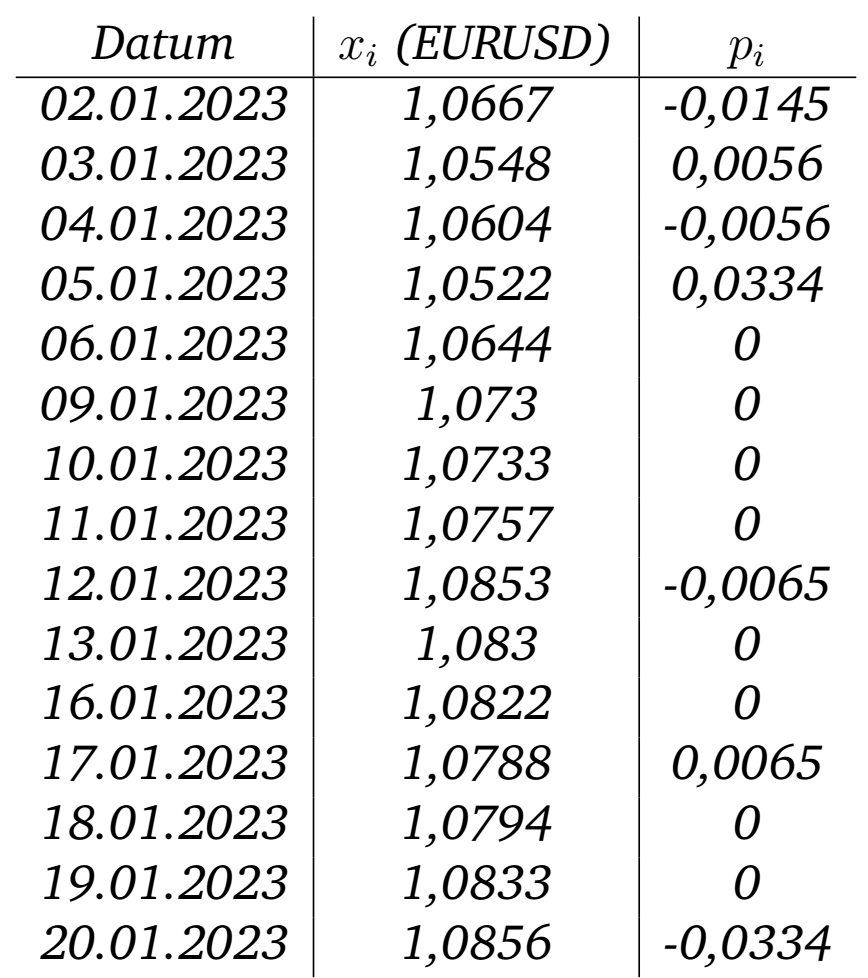
Nach Schritt 1 des Algorithmus wurden keine Daten eliminiert. Schritt 2 hat alle Punkte eliminiert, die in einem Minitrend lagen (diese haben \(p_i=0\)).
IV. Bewegungspotential
Ist die unterliegende Zeitreihe beispielsweise ein Aktienkurs, so könnte ein perfekter Prophet zum jeweiligen Zeitpunkt die Aktie kaufen oder Leerverkaufen. Sein Ertrag wäre das Bewegungspotential der Zeitreihe, das wie folgt definiert wird:
Definition 2. Für eine Zeitreihe \(X=\{x_1, \cdots, x_n\}\), \(n\in \mathbb{N}\) heißt \[P(X) = \sum_{i=1}^{n-1} \left|x_{i+1}-x_{i}\right|\] Bewegungspotential von \(X\).
In obigen Beispiel 1 ist \(P(X) = 0,0721\), d.h. ein perfekter Prophet hätte - ohne Transaktionskosten - mit 1 USD zwischen 02.01.2023 und 20.01.2023 7,21 ct erwirtschaftet. Das Bewegungspotential lässt sich auch über die Trendumkehrpotentiale darstellen, wie folgender Satz zeigt:
Satz 3. Für das Bewegungspotential \(P(X)\) für eine Zeitreihe \(X\) mit \(x_{\max}\) größter und \(x_{\min}\) kleinster Wert aus \(X\) gilt: \[P(X) = \sum_{i=1}^{n} \left|p_i\right| - \left(x_{\max} -x_{\min}\right)\]
Beweis. Nach Konstruktion des Algorithmus bleiben am Ende \(x_{\max}\) und \(x_{\min}\) übrig. Diesen wird das Potential \(x_{\max}-x_{\min}\) bzw. \(x_{\min}-x_{\max}\) zugeweisen. Diese Spannweite geht daher zweimal in die Summe ein und muss somit einmal durch Subtraktion von \(x_{\max}-x_{\min}\) korrigiert werden. Die restlich Potentialwerte entsprechen in Summe nach Konstruktion \(\sum_{i=1}^{n-1} \left|x_{i+1}-x_{i}\right|\). □
Nach obigen Beispiel 1 ist \(\sum_{i=1}^{n}
\left|p_i\right| = 0,1055\).
\(x_{\max}\) ist 1,0856 und \(x_{\min}\) ist 1,0522 und damit
0,1055-(\(x_{\max}-x_{\min}\))= 0,0721.
Dies entspricht dem Bewegungspotential.
Je später die Punkte im Algorithmus eliminiert werden, desto größer ist ihr Trendumkehrpotential \(p\). Betrachtet man in einer Zeitreihe \(X\) nur Punkte, deren Trendumkehrpotential im Absoultwert eine bestimmte Schwelle \(f\) überschreiten, kann die Zeitreihe auf ihre wesentlichen Punkte reduziert werden:
Definition 4. Sei \(X=\{x_1, \cdots, x_n\}\), \(n\in \mathbb{N}\) eine Zeitreihe und \(f>0\). Weiter sei \[T^f = \left\{i \left| |p(x_i)| > f\right.\right\}.\] Dann heißt \[X^f = \{x_i | i \in T^f\}\] die \(f\)-Filterreihe von \(X\).
Die \(f\)-Filterreihe für \(f=0,006\) aus obigem Beispiel 1 ist in folgender Tabelle dargestellt:
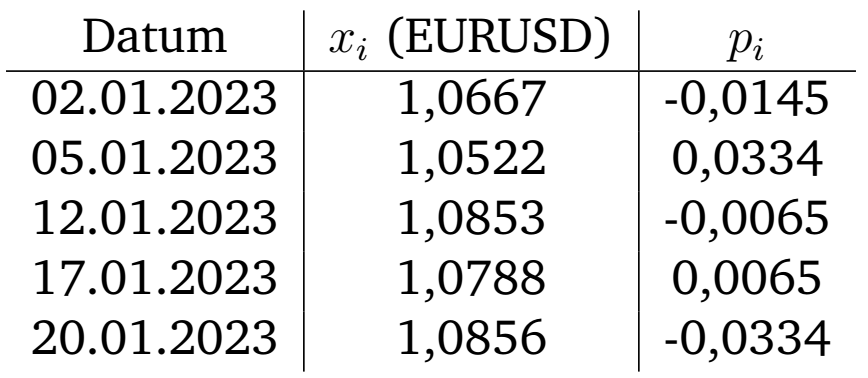
Das Bewegungspotential von \(X^f\) ist nun 0,0609. Dies wird auch \(f\)-Potential genannt.
V. Beispiel Aktienzeitreihe
Durch die Anwendung auf Aktienzeitreihen können entweder Intraday oder für längere Zeithorizonte entsprechende Potential berechnet werden. Die Zeitpunkte des Trendumkehrs kann mit anderen Zeitreihen verglichen werden. Über maschinelles Lernen können so Muster erkannt werden (z.B. systematisches "Vorlaufen" einer Zeitreihe zu einer anderen.
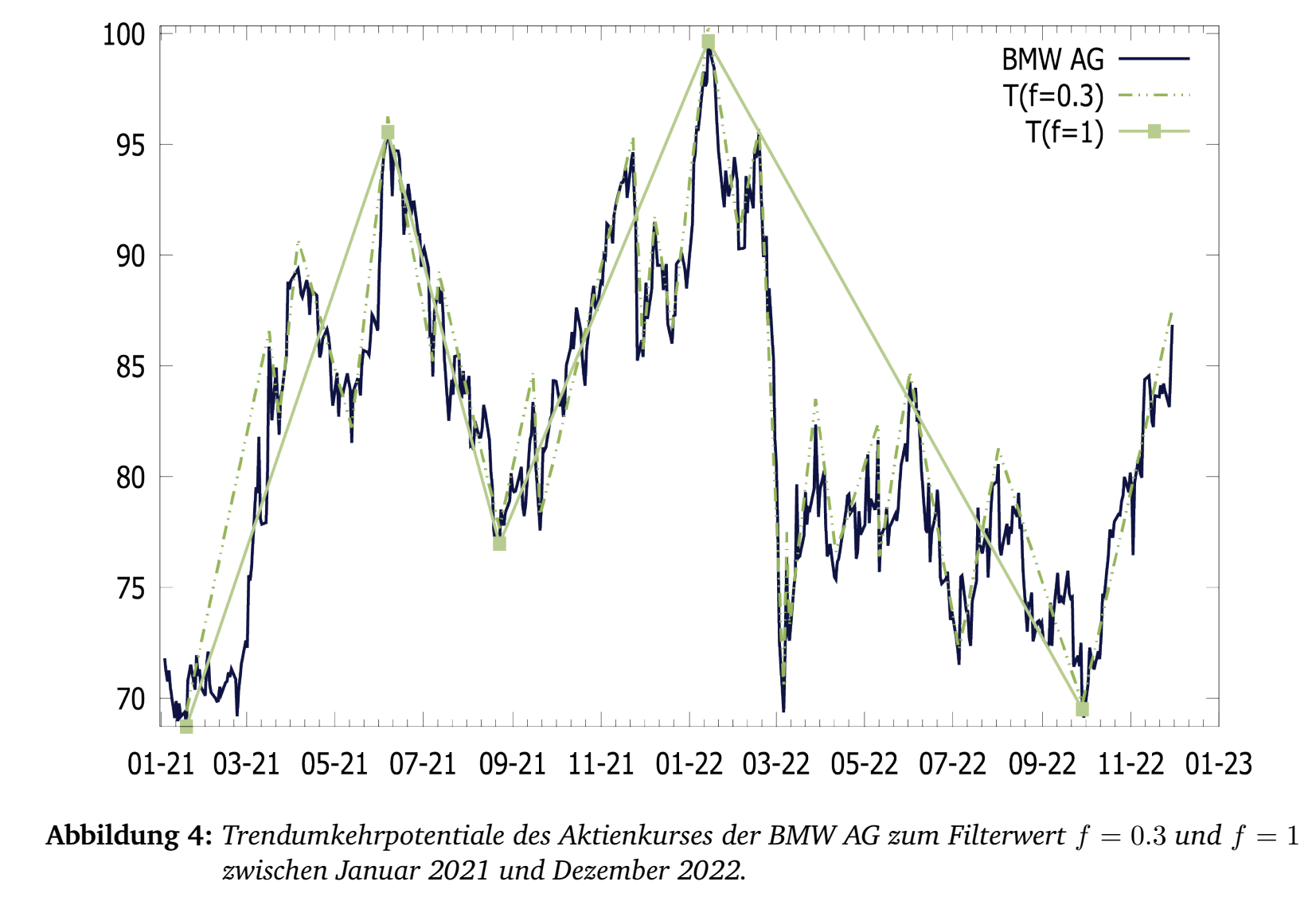
VI. Literatur
Schlittgen, Rainer, and Bernd H. J. Streitberg. 1995. Zeitreihenanalyse. München: Oldenbourg Wissenschaftsverlag.
Wegscheider, K. 1993. “Hierachische Trends.” Habitulationsschrift an der Universität Hamburg.