Self Organizing Maps (SOM)
SOMs sind im allgemeinen sehr rechenintensiv. Die rasante Entwicklung bei Rechnerleistung (u.a. GPUs) und entsprechende Programmiermöglichkeiten (z.B. miniSOM_gpu mit pyTorch) ermöglichen diesen Netzen aber eine Renaissance.
Beschreibung eines SOM
Ausgangspukt einer selbstorganisierenden Karte (SOM) ist eine fest definierte Struktur von Neuronen und eine Nachbarschaftsbeziehung der Neuronen zueinander. Meist unterschiedet man folgende Topologien:
Jedes Neuron hat zudem einen n-dimensionalen Lerngewichtsvektor (n ist die Dimension der zu lernenden Traingsmenge). Dieser Lerngewichtsvektor wird während des Lernens verändert, die Topologie dagegen bleibt unverändert.
Zweck der Topologie ist, die Nachbarschaftsbeziehung der Neuronen untereinander zu fixieren. Jedes Neuron hat dabei einen festen Abstand zu den anderen Neuronen. Der Abstand ist von der Lernmenge und der zu lerndenen Dimension unabhängig und wird auch während des Lernvorgangs nicht verändetrt. Er hängt einzig von der gewählten Topologie im Vorfeld des Lernens ab.
Beizeichnet man mit \( k_s \) die Koordinaten des Neuron \( s\) in der topoplogischen Karte (z.B. \( k_s = (x_s, y_s)=(1,3)\)) , dann ist der Abstand zum Neuron \( i \) abhängig von der im Vorfeld gewählten Topologie wie folgt:
- Rechteckig: \[ d_A(k_s, k_i) = |x_s - x_i| + |y_s - y_i| \]
- Hexagonal: \[ d_A(k_s, k_i) = \max(|x_s - x_i|, |y_s - y_i|) \]
- Ringförmig (\(N\) Neuronen): \[ d_A(k_s, k_i) = \min(|k_s - k_i|, N - |k_s - k_i|) \]
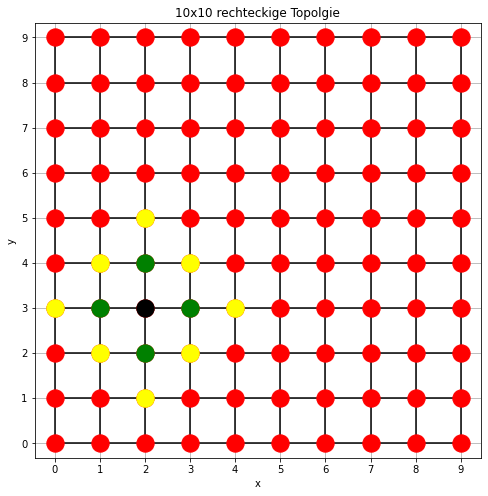
Für die rechteckige Toplogie sind nachfolgend die Neuronen mit Abstand 1 (grün) und Abstand 2 (gelb) zum Neuron (2,3) dargestellt:
Die Idee des Algorithmus von Kohonen ist nun, einen Punkt P aus der Traingsmenge zufällig auszuwählen.
Das Neuron, dessen Gewichte am nächsten zum Punkt P liegt (gemessen mit der euklidischen Distanz), wird ausgewählt (=Best Matching Unit oder BMU). Die Gewichte des BMU-Neurons werden nun so angepasst, dass sie näher beim Punkt P liegen (wie nah hängt von einer Lernrate ab).
Gleichzeitig werden die Gewichte der Neuronen, die dem BMU am nächsten liegen (gemessen mit dem topologischen Abstand) ebenso in Richtung des Punktes P angepasst. Dabei werden werden weiter weg liegende Neuronen weniger und nähere Neuronen stärker angepasst.
Im Laufe des Algorithmus werden die Lernrate und die Gewichtsanpassungen der topologischen Nachbarneuronen reduziert.
Beispiel: einfaches SOM
Im folgenden kurzen Video sind die Gewichte (und nicht die Koordinaten) der Neuronen eines 1x150-Netzes dargestellt. Die schwarzen Verbindungslinien zeigt den Nachbarschaftsbezug. Die Trainigsmenge sind die grauen Punkte im Kreisring. Zu Beginn sind die Gewcihte der Neuronen zufällig belegt. Bei jeder Iteration wird aus der Traingsmenge zufällig ein Punkt (schwarz) ausgewählt und das Neuron, dessen Gewichte am nächsten liegt, bestimmt (rot). Beides sieht man am Besten, wenn man das Video kurz pausieren lässt.
Die Gewichte von benachbarten Neuronen werden ebenfalls zu dem Punkt "gezogen". Dieser Effekt wird im Laufe der Iteration mit abnehmender Lernrate und abnehmendem sigma kleiner. Im Laufe der Iterationen passen sich die Gewichte immer mehr dem Kreisring an. Die Topologie (das sind die Verbindungen zwischen den Neuronen) bleibt erhalten.
Algortihmus
Input:
\( T \): Trainingsmenge, \( T
= \{x_i \in \mathbb{R}^n \mid i = 1, \dots, \mu_T\} \)
\( k_x, k_y \): Dimensionen der Karte (z. B. \( 10 \times 10 \))
Topologie: Rechteckig oder hexagonal oder Ringförmig
\( t_{\text{max}} \): Maximale Anzahl der
Iterationen
\( \epsilon(t) \): Lernraten-Decay-Funktion, die die
Lernrate \( \epsilon(t) \) mit der Zeit reduziert
\( \delta(t) \): Nachbarschafts-Decay-Funktion
\( d_X \): Abstandsfunktion im Inputraum (z.B.
euklidische Norm))
\( d_A \): Abstandsfunktion auf der Karte, abhängig von
der Topologie
Output:
Gelerntes neuronales Netz \( SOM \) (bestehend aus
Gewichtsvektoren \( w_i \) ).
Initialisierung:
Die Karte wird als \( k_x \times k_y \) Gitter
definiert, wobei jede Position \( k_i = (x, y) \)
eindeutig durch natürliche Zahlen bestimmt ist: \( x \in
\{0, \dots, k_x-1\} \), \( y \in \{0, \dots,
k_y-1\} \).
Alle Gewichtsvektoren \( w_i \in \mathbb{R}^n \)
werden zufällig initialisiert.
Die Abstandsfunktion \( d_A(k_s, k_i) \) hängt von
der gewählten Topologie ab (siehe oben).
Lernphase: \( t=1 \text{ bis } t_{\text{max}}
\)
- Ziehe \( x_t \in T \) zufällig aus der Trainingsmenge.
- Finde das Neuron \( n_s \) (BMU) mit dem kleinsten Abstand im Inputraum: \[ n_s = \arg\min_{n_i \in N} \|x_t - w_i\| \] Hierbei ist \( n_s \) das Neuron, dessen Gewichtsvektor \( w_s \) dem Trainingsvektor \( x_t \) am nächsten liegt.
- Definiere die Nachbarneuronen \( N^+(t) \), basierend auf der Topologie und dem Nachbarschaftsradius \( \delta(t) \): \[ N^+(t) = \{n_i \in N \mid d_A(k_s, k_i) \leq \delta(t)\} \] Die Nachbarschaftsgewichtung \( h_{si}(t) \) wird durch eine Gauß-Funktion bestimmt: \[ h_{si}(t) = e^{-\frac{d_A(k_s, k_i)^2}{2 \cdot \delta(t)^2}}. \]
- Für jedes Neuron \( n_i \in N^+(t) \) passe den Gewichtsvektor \( w_i \) an: \[ w_i(t+1) = w_i(t) + \epsilon(t) \cdot h_{si}(t) \cdot (x_t - w_i(t)). \] Hierbei sind \( \epsilon(t) \) die Lernrate und - \( h_{si}(t) \) die Nachbarschaftsgewichtung. Beide reduzieren sich mit \( t \) gemäß ihrer Decay-Funktion.
Anwendungsphase:
Nach Abschluss der Lernphase kann die Karte verwendet werden, um neue Stimuli \( x \) zu klassifizieren. Ein neuer Stimulus wird dem Neuron zugeordnet, dessen Gewichtsvektor den geringsten Abstand zu \( x \) aufweist: \[ n_s = \arg\min_{n_i \in N} \|x - w_i\|. \]