Zur besseren Verständlichkeit wird im Folgenden ein 3-dimensionaler Datenraum verwendet. Das Prinzip ist aber auf beliebige endliche Dimensionen anwendbar.

In einem dreidimensionalen Raum ist jeder Punkt durch Koordinaten wie \((x_1,x_2,x_3) \in \mathbb{R}^3\) bezeichnet. Diese Koordinaten beschreiben den Punkt als Linearkombination der Standardbasisvektoren: \[x_1 \cdot e_1 + x_2 \cdot e_2 + x_3 \cdot e_2 = x_1\cdot\left(\begin{array}{c} 1\\0\\0\end{array}\right)+x_2\cdot\left(\begin{array}{c} 0\\1\\0\end{array}\right)+x_3\cdot\left(\begin{array}{c} 0\\0\\1\end{array}\right)\] Eine Menge von Vektoren heißt Basis, wenn aus ihr alle Punkte des Raumes über Linearekombinationen darstellbar sind (Erzeugendensystem) und sich kein Basisvektor über Linearkombinationen der anderen Basisvektoren darstellen lässt (linear unabhängig).

Basiswechsel

Die Anzahl der Basisvektoren entspricht im endlichen Fall immer der Dimension des Raumes (in unserem Besipiel 3). Es gibt unendlich viele Möglichkeiten, eine Basis auszuwählen. Wird beispielsweise anstelle von \(e_1, e_2, e_3\) eine andere Basis verwendet, z.B. \(v_1, v_2, v_3\), dann ändern sich auch die Koordinaten \((x_1,x_2,x_3)\) des ausgewählten Punktes,

Beispiel: Angenommen wir betrachten die neue Basis \[v_1=\left(\begin{array}{c} 1\\1\\0\end{array}\right), v_2=\left(\begin{array}{c} 0\\2\\0\end{array}\right),v_3=\left(\begin{array}{c} 1\\0\\1\end{array}\right)\] Der Punkt \((1,1,1)^T\) auf Basis der Standardbasis entspricht dann dem Punkt \((0,0.5,1)^T\) für die Basis \(v_1, v_2, v_3\), da \[0\cdot\left(\begin{array}{c} 1\\1\\0\end{array}\right)+0.5 \cdot \left(\begin{array}{c} 0\\2\\0\end{array}\right)+1\cdot \left(\begin{array}{c} 1\\0\\1\end{array}\right) = \left(\begin{array}{c} 1\\1\\1\end{array}\right)\] Der Übergang von \((1,1,1)^T\) von der Standardbasis auf \((0,0.5,1)^T\) in der Basis \(v_1, v_2, v_3\) heißt Basiswechsel.

Principal Component Analysis

Wenn wir viele Punkte (Daten) im Raum haben, können wir eine Basis so wählen, dass sie die Struktur der Daten besser beschreibt. Die Idee der PCA ist, eine Basis zu finden, bei der:

1. Der erste Basisvektor \(v_1\) die meiste Varianz der Daten erklärt, d.h. die Hauptstreurichtung der Daten ist.

2. Der zweite Basisvektor \(v_2\) orthogonal (also senkrecht bzw. das Skalarprodukt ist 0) zu \(v_1\) ist und die zweitmeiste Varianz der Daten erklärt.

3. Der dritte Basisvektor \(v_2\) orthogonal zu den beiden anderen ist und die restliche Varianz erklärt.

Das Ergebnis ist eine neue Orthogonalbasis, die optimal auf die Verteilung der Daten abgestimmt ist.

Vorgehen

Die PCA beginnt damit, die Daten zu zentrieren. Dazu wird der Mittelwert jeder Dimension von allen Punkten subtrahiert, sodass der Datensatz um den Ursprung zentriert ist.

Danach wird die Varianz-Kovarianz-Matrix berechnet. Diese Matrix beschreibt, wie die Dimensionen miteinander variieren und gibt Aufschluss über die Streuung der Daten in verschiedenen Richtungen.

Im nächsten Schritt erfolgt die Eigenwertzerlegung der Varianz-Kovarianz-Matrix. Dabei werden die Eigenvektoren und Eigenwerte berechnet. Die Eigenvektoren sind die neuen Basisvektoren, welche die Richtung der maximalen Datenstreuung angeben. Die zugehörigen Eigenwerte geben an, wie viel Varianz jeder Basisvektor erklärt. Die Varianz-Kovarianz-Matrix ist symmetrisch und positiv-semidefinit, d.h. alle Eigenwerte sind größer gleich 0 und reell und die zugehörigen Eigenvektorn sind orthogonal (Spektralsatz).

Die Eigenvektoren werden anschließend nach den absteigenden Eigenwerten sortiert. Der Eigenvektor mit dem größten Eigenwert wird zur ersten Hauptkomponente, da er die meiste Varianz der Daten erklärt. Der zweite Eigenvektor mit dem nächstgrößten Eigenwert wird zur zweiten Hauptkomponente und so weiter.

Zuletzt werden die ursprünglichen Daten in die neue Basis projiziert (Basiswechsel). Dies geschieht, indem die Datenpunkte auf die Hauptkomponenten abgebildet werden. Die neuen Koordinaten in dieser Basis beschreiben die Position der Datenpunkte in Bezug auf die Hauptkomponenten. Diese neuen Koordinaten ermöglichen eine reduzierte Darstellung der Daten, die die wichtigsten Variationen beibehält.

Beispiel

Wir haben nachfolgende 3-diemsionale Punktmenge (Excel mit den Daten ist hier). Die Punkte haben ein Farblabel. Die Punktmengen unterschiedlicher Farbe sind disjunkt (mit der Maus kann man die Grafik drehen und sich davon überzeugen). Zudem sind die Punkte auf den Bereich \([0,1]^3\) skaliert (ansonsten wäre eine Skalierung empfehlenswert).

Die Varianz-Kovarianz-Matrix der Daten ist: \[ \begin{pmatrix} 0.04329899 & 0.01879311 & -0.00609738 \\ 0.01879311 & 0.03883577 & 0.02490926 \\ -0.00609738 & 0.02490926 & 0.04825152 \end{pmatrix} \] Hieraus können nun die Eigenvektoren (normiert auf Länge 1) und die zugehörigen Eigenwerte ermittelt werden: \[ \begin{aligned} \text{Eigenwert } \lambda_1 &= 0.07134679, \quad \text{Eigenvektor } v_1 = \begin{pmatrix} 0.31673124 \\ 0.6854283 \\ 0.6556442 \end{pmatrix}, \\ \text{Eigenwert } \lambda_2 &= 0.05072934, \quad \text{Eigenvektor } v_2 = \begin{pmatrix} 0.82204473 \\ 0.14648707 \\ -0.55025816 \end{pmatrix}, \\ \text{Eigenwert } \lambda_3 &= 0.00831015, \quad \text{Eigenvektor } v_3 = \begin{pmatrix} -0.47320592 \\ 0.7132528 \\ -0.5170557 \end{pmatrix}. \end{aligned} \] Eine Varianz-Kovarianz-Matrix ist immer symmetrisch. Daher sind alle Eigenwerte reell und nicht kleiner 0 (positiv semi-definit). Die Eigenvektoren bilden eine Orthogonalbasis, d.h. das Skalarprodukt zweier beliebiger Eigenvektoren ist 0.

Bildet man aus den Eigenvektoren die Matrix \[ P = \begin{pmatrix} 0.31673124 & 0.82204473 & -0.47320592 \\ 0.6854283 & 0.14648707 & 0.7132528 \\ 0.6556442 & -0.55025816 & -0.5170557 \end{pmatrix} \] dann ist \[ P^{-1}=P^T= \begin{pmatrix} 0.31673118 & 0.6854283 & 0.65564424 \\ 0.8220447 & 0.14648703 & -0.55025816 \\ -0.47320592 & 0.71325284 & -0.5170557 \end{pmatrix} \]

Das Produkt von \(P\) mit seiner Transponierten ergibt somit die Einheitsmatrix, was die Orthonormalität der Eigenvektoren bestätigt.

In der nachfolgenden Darstellung ist die Punktmenge mit den neuen Koordinaten bezüglich der Basis mit den drei Eigenvektoren (PC=Principial Components). PC1 ist dabei der Eigenvektor zum größten Eigenwert und PC3 derjenige zum kleinsten Eigenwert.

Die Daten sind in ihrer Form identisch zur Ausgangslage (einfach mit der Maus die Daten drehen). Allerdings haben sich die Achsen und der Koordinatenmittelpunkt im Raum verschoben. Die Achse PC1 gibt die Richtung der größten Streuung der Datenpunkte an, PC2 zeigt die Richtung der zweit größten Streuung. Die drei Aschen stehen nach wie vor senkrecht aufeinander (orthogonal).

Interssanter ist nun die Projektion der Daten auf die zwei Hauptkomponenten PC1 und PC2 (links) im Vergleich zur Projektion auf die ursprüngliche X-Y-Ebene (rechts), d.h. es werden in beiden Fällen nur die Koordinataten der ersten beiden Basen verwendet:

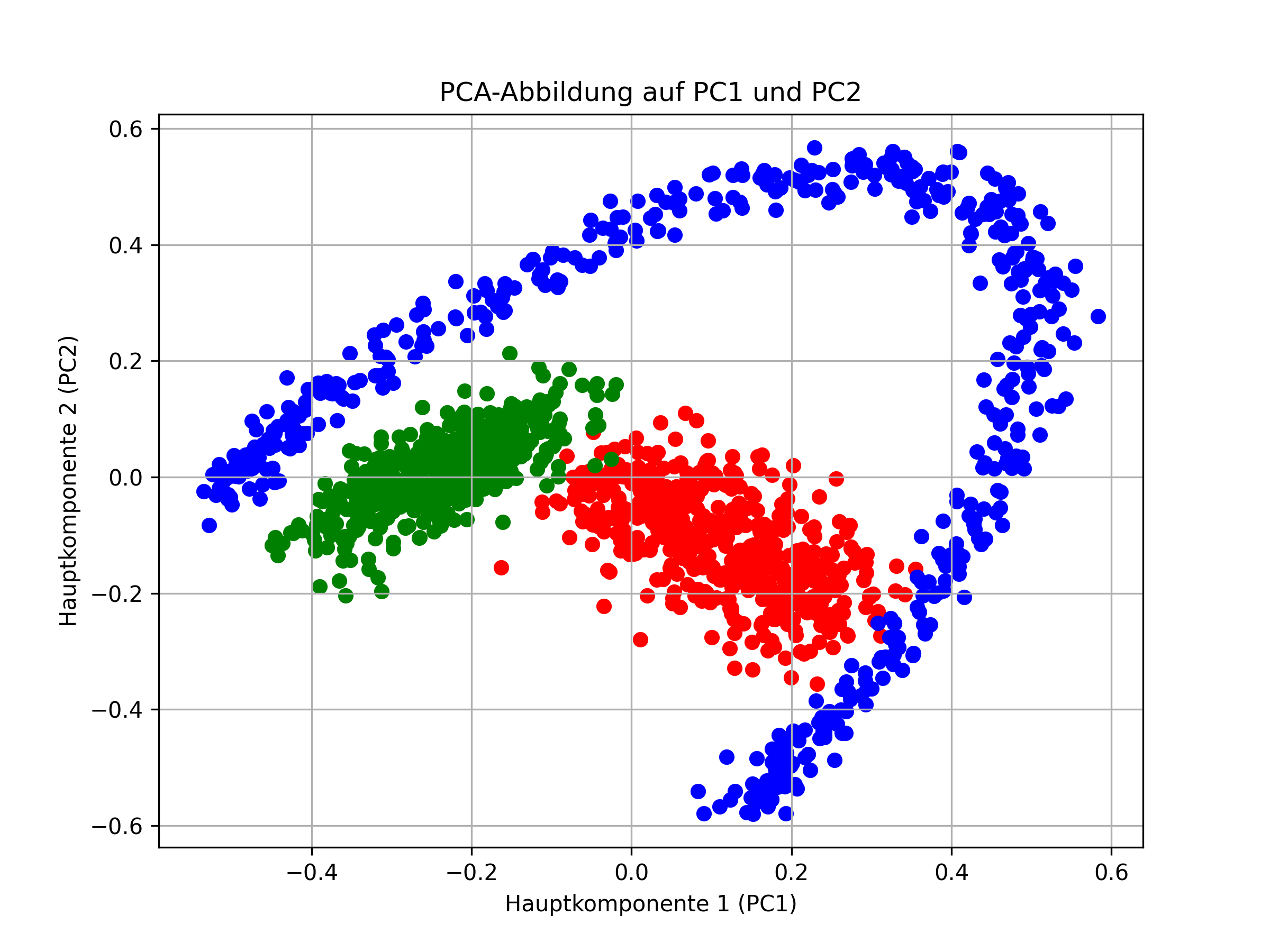
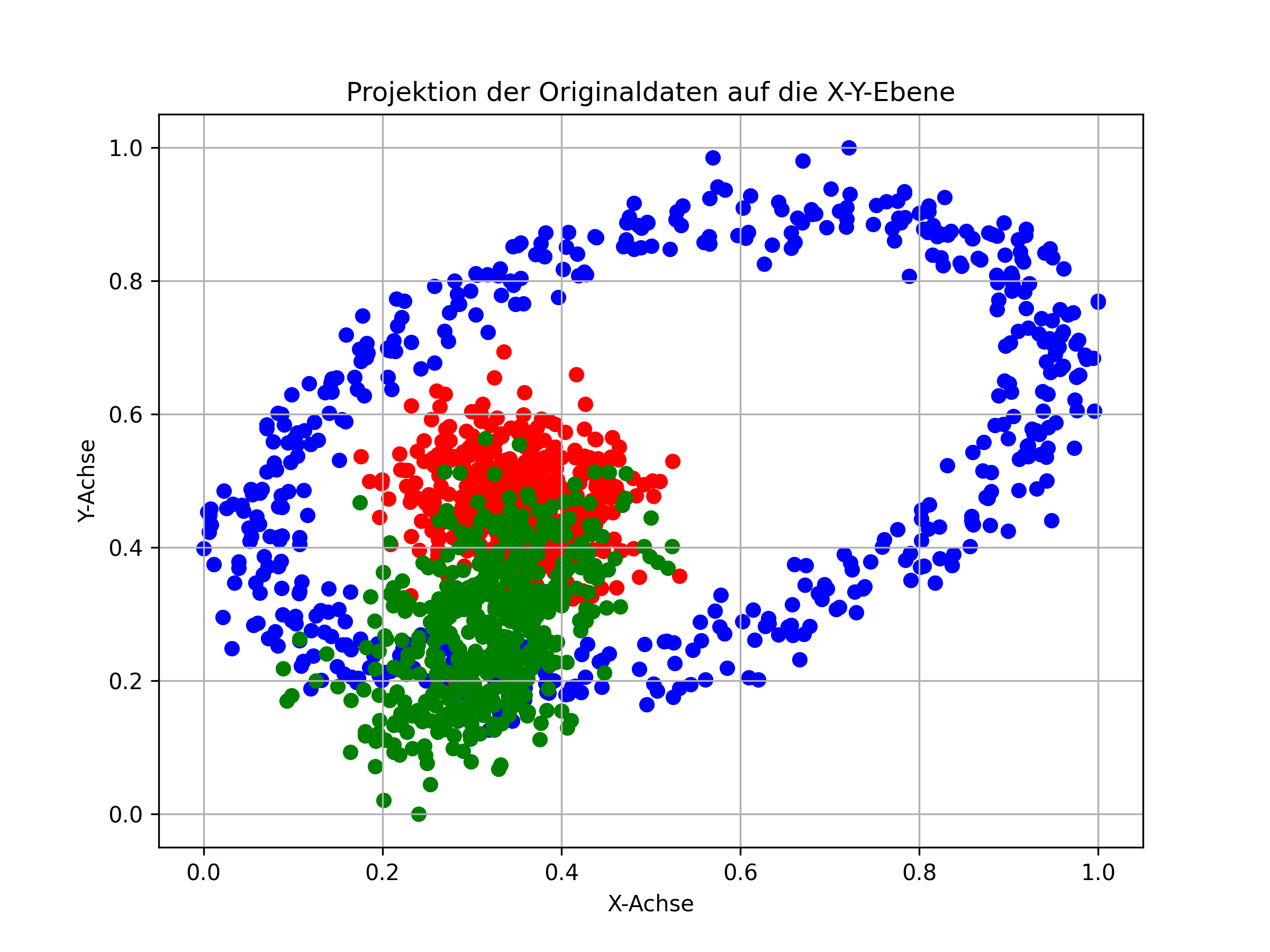
Die PCA-Projektion auf die beiden Hauptkomponenten bildet die Datenstruktur wesentlich besser ab. Hier könnte ein einfaches neuronales Netz eine Trennung der Datenmengen vornehmen.

Die PCA-Projektion auf die zwei Hauptkomponenten kann mit der Matrix P wieder auf die Stanard-Basis übertragen werden. Die Datenstruktur ist hier um die dritte Hauptkomponente bereinigt (evtl. Störterme)

Anwendungen

Die Principal Component Analysis (PCA) oder Hauptkomponentenanalyse hat zahlreiche Einsatzmöglichkeiten:

1. Dimensionsreduktion: PCA kann die Dimension von Daten reduzieren. Dies ist nützlich, um hochdimensionale Daten für Neuronale Netze oder andere Analysetools handhabbarer zu machen und unerwünschtes Datenrauschen zu entfernen. Je nach Anzahl der verwendeten Hauptkomponenten bleibt die meiste Varianz der Daten enthalten, nämlich: \[\frac{\sum_{i=1}^p\lambda_i}{\sum_{i=1}^n\lambda_i}\cdot 100 \%\] Dabei sind \(\lambda_i, i=1 \dots n\), die absteigend sortierten Eigenwerte, \(n\) die Dimension der Ursprungsdaten und \(p\) die Anzahl der verwendeten Hauptkomponenten.

   
   Nach Dimensionsreduktion können die Daten visualisiert werden (2D oder 3D), als Input für Analysealgortimhen oder Neuronale Netze dienen oder die Daten mit Hilfe der Belegung auf den Hauptkomponenten direkt analysiert werden.

2. Datenkompression: PCA kann Daten komprimieren, indem weniger Hauptkomponenten gespeichert werden - je nach Wahl der Anzahl der Hauptkomponenten kann dies ohne signifikanten Informationsverlust erfolgen. Der Grad der Information in der Komprimierung kann dabei wieder über \[\frac{\sum_{i=1}^p\lambda_i}{\sum_{i=1}^n\lambda_i}\cdot 100 \%\] berechnet werden.

   Möchte man beispielsweise ein Schwarzweißbild X mit (3200x2000) Pixel komprimieren, so besteht das Bild aus 3200 Zeilen (=Datensätze mit Graustufen) und 2000 Dimensionen (=Spalten). Man kann nun die ersten 50 Hauptkomponenten P (2000x50) berechnen . Zudem speichert man zu jedem Datensatz die jeweiligen Koordinataten bzgl. der 50 Vektoren W (3200x50). Zur Rekonstruktion des um Rauschen/Information reduzierten Bildes multipliziert man \(W P^T=X_{\text{reduz.}}\). Der Speicherbedarf ist nun \(2000 \cdot 50 (=P) + 3200\cdot 50 (=W)\) und damit rund 24x kleiner als für das Ursprungsbild.