Für \(a \in \mathbb{R}^n\)
bezeichnet \(a_i\) die \(i\)-te Vektorkomponente. Bei Vektoren sind
\(<, \leq, >, \geq, =, \neq\)
komponenteweise zu verstehen, d.h. für \(a \in
\mathbb{R}^n\) bedeutet \(a>0\), dass \(a_i > 0\) für alle \(i=1,
\dots, n\) gilt. \(1_n\) bezeichnet den Vektor
\((1, \dots, 1)^T\) aus \(\mathbb{R}^n\). \(0_n\)
wird analog definiert.
Im Folgenden werden nun endliche Punktmengen \({\cal A} =
\{a^{(1)}, \dots, a^{(m)}\}\)
und \({\cal B} = \{b^{(1)}, \dots,
b^{(k)}\}\) aus \(\mathbb{R}^n\)
betrachtet. Mit \(A=[a^{(1)}, \dots,
a^{(m)}]^T \in \mathbb{R}^{m \times n}\) und \(B=[b^{(1)}, \dots, b^{(k)}]^T \in \mathbb{R}^{k
\times n}\) werden die Matrizen betrachtet, deren Zeilen die
einzelenen Punkte aus \({\cal A}\) bzw.
\({\cal B}\) darstellen.
Linear trennbare Punktmengen
\({\cal A}\) und \({\cal B}\) sollen trennbar heißen, wenn ihre konvexen Hüllen \(\text{conv}({\cal A})\) bzw. \(\text{conv}({\cal B})\) trennbar sind. Falls endliche Punktmengen trennbar sind, sind diese stets strikt trennbar, da \(\text{conv}({\cal A})\) und \(\text{conv}({\cal B})\) kompakt und abgeschlossen sind.
Satz 1. \({\cal A}\) und \({\cal B}\) sind genau dann trennbar, wenn fogendes Lineares Programm eine positive Lösung hat: \[\begin{array}{rl} \text{Maximiere} & \alpha - \beta\\ \text{u.d.B.} & A c - \alpha 1_m \geq 0\\ & -B c + \beta 1_k \geq 0\\ & 1_n \geq c \geq -1_n. \end{array}\]
Proof. siehe pdf.
Durch das Lineare Programm werden bei trennbaren Punktmengen \({\cal A}\) und \({\cal
B}\) zwei parallele Hyperbenen \(E_1 = \{x \in
\mathbb{R}^n | c^T x =
\alpha\}\) und \(E_2 = \{x \in
\mathbb{R}^n | c^T x = \beta\}\) erzeugt. \(E_1\) bzw. \(E_2\) haben
mindestens einen Punkt mit \({\cal A}\) bzw. \({\cal B}\) gemeinsam. Zudem ist der Abstand
der beiden Hyperebenen wegen der Zielfunktion \(\alpha-\beta\) maximal. Die Hyperebene
\(E = \{x \in \mathbb{R}^n | c^T x =
\frac{\alpha+\beta}{2}\}\) ist eine "’optimale"’ Hyperebene zum
Trennen der Punktmengen.
Satz 2. Das Lineare Programm lässt sich in die Form \[\begin{array}{rl} \text{Maximiere} & d^T x\\ \text{u.d.B.} & D x \leq b\\ & x \geq 0 \end{array}\] überführen.
Proof. Zur Vereinfachung der Notation wird mit \(0_n = (0,\dots , 0)^T\) der Nullvektor in
\(\mathbb{R}^n\) bezeichnet und mit
\(I_n\) die Identitätsmatrix aus \(\mathbb{R}^{n\times n}\).
Zunächst muss \(x \geq 0\)
erfüllt sein. Hierzu wird aus \(c = c^+ -
c^-\), \(\alpha = \alpha^+ -
\alpha^-\) und \(\beta = \beta^+ -
\beta^-\) mit \(c^+, c^-, \alpha^+,
\alpha^-,\beta^+, \beta^- \geq 0.\) Der gesuchte Vektor \(x\) ist dann \(x=((c^+)^T,\alpha^+,\beta^+,(c^-)^T,
\alpha^-,\beta^-)^T \in \mathbb{R}^{2n+4}\) und \(d=((0_n)^T, 1,-1,(0_n)^T, -1,1)^T\in
\mathbb{R}^{2n+4}\).
Die Bedingung \(1_n \geq c \geq
-1_n\) wird zu \(c^+ - c^- \leq
1_n\) und \(-c^+ + c^- \leq
1_n\). Die Matrix \(D \in
\mathbb{R}^{(2n+m+k) \times (2n+4)}\) lässt sich folgendermaßen
schreiben: \[D= \left(
\begin{array}{rrrrrr}
-A & 1_m & 0_m & A & -1_m & 0_m\\
B & 0_k & -1_k & -B & 0_k & 1_k\\
I_n & 0_n & 0_n & -I_n & 0_n & 0_n\\
-I_n & 0_n & 0_n & I_n & 0_n & 0_n
\end{array}
\right)\] und \(b\) ist \(((0_m)^T, (0_k)^T,(1_n)^T, (1_n)^T)^T\) mit
\(b \in \mathbb{R}^{2n+m+k}\). ◻
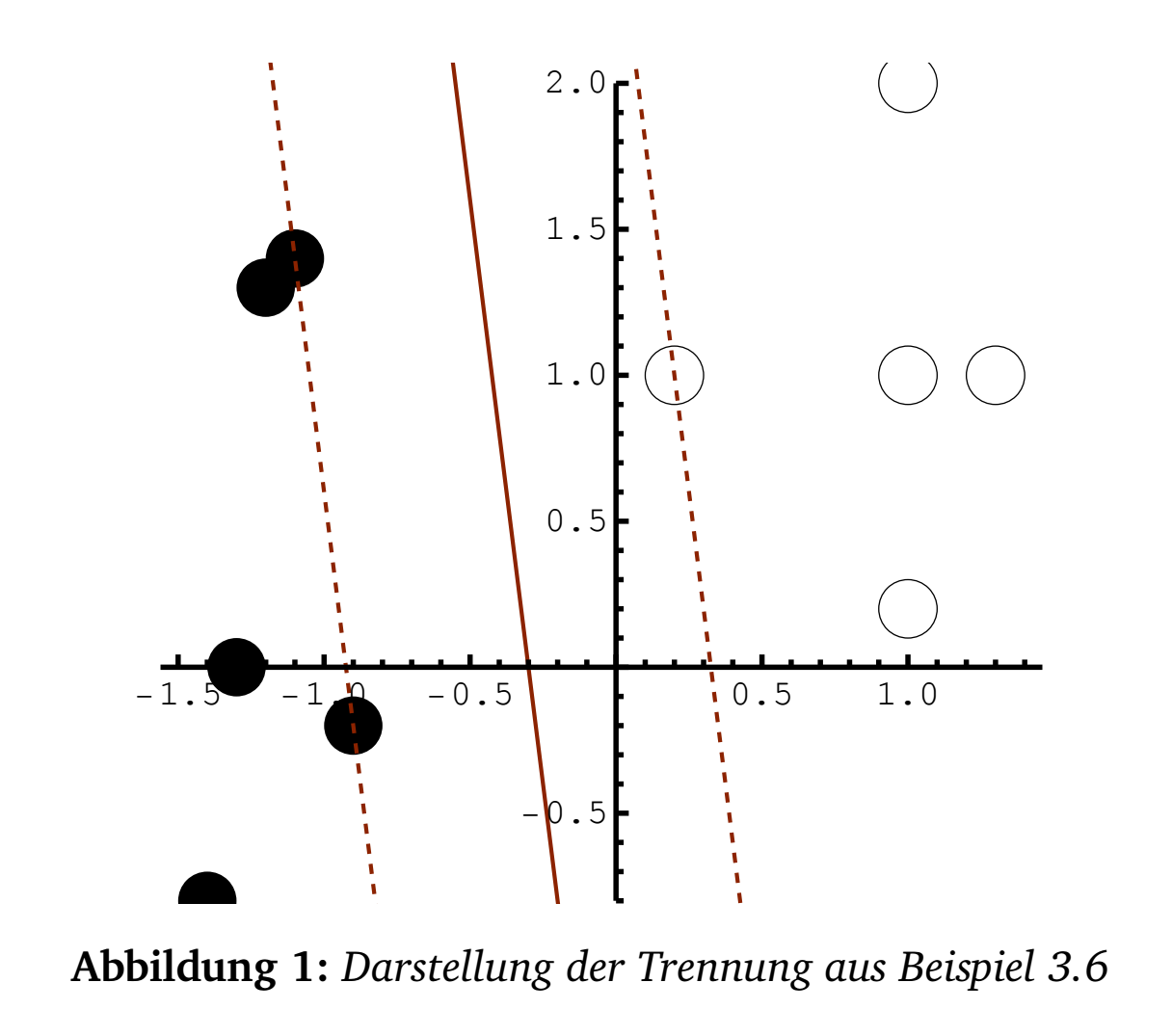
Beispiel 3. Es sollen die Mengen \({\cal A} = \{(1, 1)^T, (0.2, 1)^T, (1, 0.2)^T,
(1.3, 1)^T, (1, 2)^T\}\) und \({\cal B}
= \{(-1.2, 1.3)^T, (-1.4, -0.8)^T, (-1.3, 0)^T,
(-0.9, -0.2)^T, (-1.1, 1.4)^T\}\) getrennt werden.
Es ist \(m=5\), \(k=5\) und \(n=2\).
Dann ist \(d=(0,0,1,-1,0,0,-1,1)^T\) und \(b = (0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1)^T\). Die Matrix \(D\) ist \[D=\left(
\begin{array}{cccccccc}
-1 & -1 & 1 & 0 & 1 & 1 & -1 & 0 \\
-0.2 & -1 & 1 & 0 & 0.2 & 1 & -1 & 0 \\
-1 & -0.2 & 1 & 0 & 1 & 0.2 & -1 & 0 \\
-1.3 & -1 & 1 & 0 & 1.3 & 1 & -1 & 0 \\
-1 & -2 & 1 & 0 & 1 & 2 & -1 & 0 \\
-1.2 & 1.3 & 0 & -1 & 1.2 & -1.3 & 0 & 1 \\
-1.4 & -0.8 & 0 & -1 & 1.4 & 0.8 & 0 & 1 \\
-1.3 & 0 & 0 & -1 & 1.3 & 0 & 0 & 1 \\
-0.9 & -0.2 & 0 & -1 & 0.9 & 0.2 & 0 & 1 \\
-1.1 & 1.4 & 0 & -1 & 1.1 & -1.4 & 0 & 1 \\
1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & -1 & 0 & 0 \\
-1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 0 & 1 & 0 & 0 \\
\end{array}
\right)\] Die Berechnung des Linearen Programm mit
Standardalgortihmen liefert für \[\begin{array}{rl}
\text{Maximiere} & d^T x\\
\text{u.d.B.} & D x \leq b\\
& x \geq 0
\end{array}\] den Lösungsvektor \(x=(1,
0.125, 0.325, 0, 0, 0, 0,0.925)^T\) und damit \[(c,\alpha,\beta) = ((1, 0.125), 0.325,0)^T - ((0,
0), 0, 0.925)^T = ((1,0.125),0.325,-0.925)^T.\] Die "’optimal"’
trennende Hyperbene von \({\cal A}\)
und \({\cal B}\) ist dann \[E=\left\{x \in \mathbb{R}^2 \left| (1,0.125) x -
\frac{0.325 - 0.925}{2}\right.\right\}.\]
Der Algortihmus 1 in Abbildung 2 fasst die Ergebnisse zusammen.

Nichtlinear trennbare Punktmengen
Falls die Punktmengen \({\cal A}\)
und \({\cal B}\) nicht trennbar sind,
liefert das lineare Programm die Lösung \(x=(0,\dots,0)^T \in
\mathbb{R}^{2n+4}\) und
damit \(c=(0, \dots, 0)^T \in
\mathbb{R}^n\).
Es ist allerdings möglich in diesem Fall eine Lösung mit \(c \neq 0\) zu erzwingen. Hierzu wird das
Lineare Programm so verändert, dass eine Komponente von \(c\) ungleich \(0\) ist.
Beispielsweise kann \(c_i = 1\) durch Veränderung von \(b\) folgendermaßen "’erzwungen"’ werden.
Sei dazu \(1_n^{(i)} = (1, \dots, 1, -1,1,
\dots,1) \in \mathbb{R}^n\) der Vektor \(1_n\)
mit \(-1\) an \(i\)-ter
Komponente. Dann ist mit \(b=((0_m)^T, (0_k)^T,(1_n)^T,
(1_n^{(i)})^T)^T\) die Nebenbedingung \(-c_i^+ + c_i^-
\leq -1\). Zugleich gilt
\(c_i^+ - c_i^- \leq 1\) unverändert,
d.h. in Summe \(c_i=c_i^+ - c_i^- =
1\). Analog ist für \(b=((0_m)^T,
(0_k)^T, (1_n^{(i)},(1_n)^T)^T)^T\) \(c_i =
-1\).
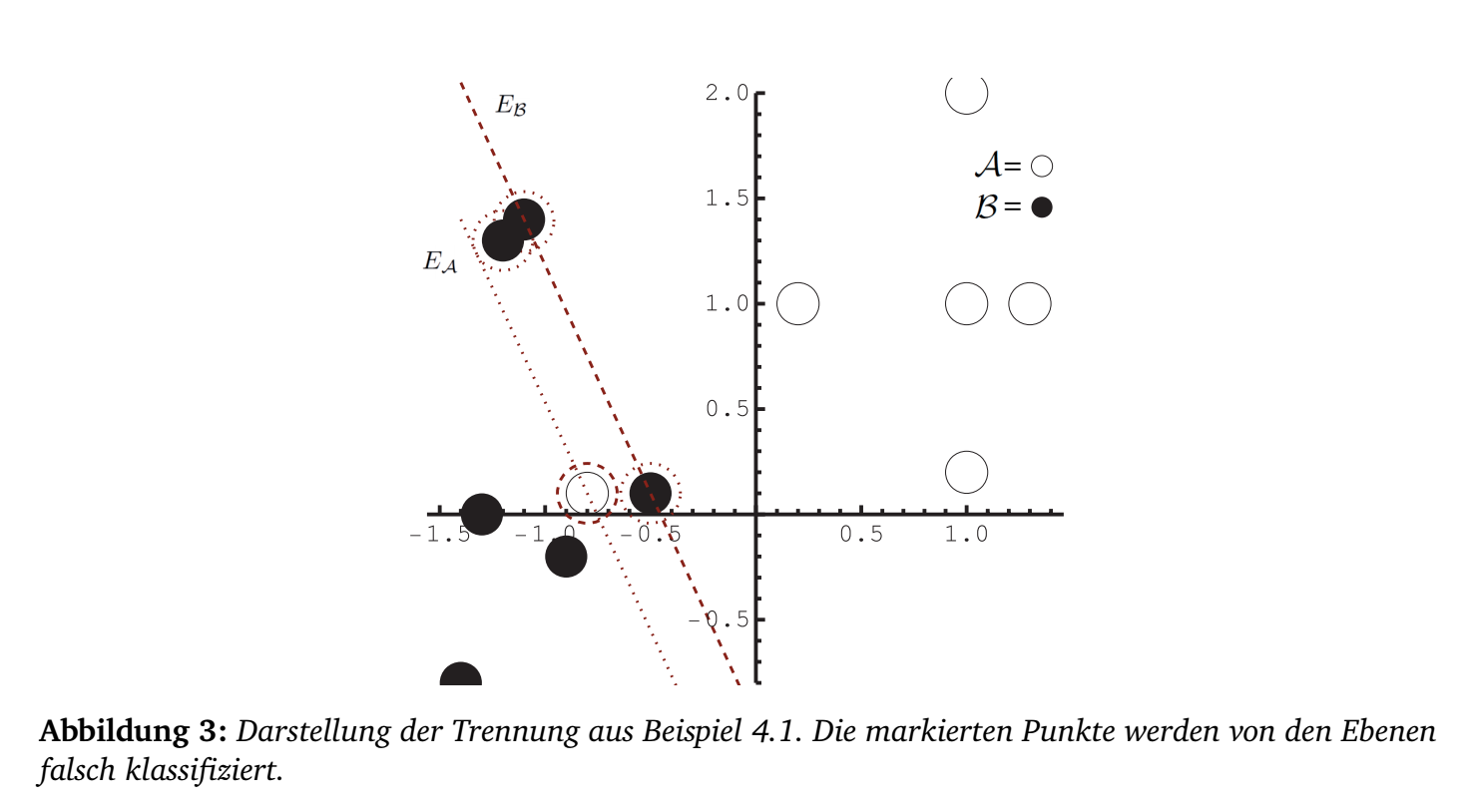
Beispiel 4. Der Punkt \((-0.8, 0.1)^T\) wird in \({\cal A}\) und \((-0.5,
0.1)^T\) in \({\cal B}\) zusätzlich
aufgenommen. Das
Lineare Programm aus Satz 2 liefert einen Nullvektor als Lösung, d.h. die
Punkte sich nicht linear trennbar. Das modifizierte Lineare Programm mit
\(c_1 = 1\) liefert folgende Lösungen:
\[\alpha=-0.753846 \text{ und }
\beta=-0.453846\] \[E_{\cal A} =
\left\{x \in \mathbb{R}^2 \left|(1.,0.461538) x =
-0.753846\right.\right\}\] \[E_{\cal
B}=\left\{x \in \mathbb{R}^2 \left|(1.,0.461538) x =
-0.453846\right.\right\}.\]
Emittle nun alle Punkte \((x_1,x_2)^T\) aus \({\cal
B}\) mit \((x_1,x_2)^T (1.,0.461538) + 0.753846
>0\) und alle Punkte \((x_1,x_2)^T\)
aus \({\cal A}\) mit \((x_1,x_2)^T (1.,0.461538) + 0.453846
<0\) (vgl. Abbildung 3) und streiche die jeweils identifizierten
Punkte aus \({\cal B}\) und aus \({\cal A}\). Dann sind die Punktmengen
trennbar. Für die gestrichenen Punkte kann ein neuer Trennungsversuch
unternommen werden. So können sukzessive alle Punkte getrennt
werden.
Durch die Variation \(c_i = \pm 1\)
für alle \(i=1, \dots, n\) lassen sich
die Ebene finden, für die die wenigsten Punkte für eine Trennung
eleminiert werden müssen. Diese eliminierten Punkte können nun neu
getrennt werden. Durch den Algorithmus 2 in Abbildung 4 können so beliebige
Punktmengen getrennt werden.

Ein unbekannter Punkt kann einer Menge eindeutig zugeordnet werden, wenn die Lösungen des Algorithmus 2 aus Abbildung 4 nach und nach angewandt werden bis eine Trennung gefunden ist (vgl. Algorithmus 3 in Abbildung 5). Dabei wird die Trennungskategorisierung zur Punktmenge \({\cal A}\) bzw. \({\cal B}\) mit höherer Trennungstiefe unschärfer und unsicherer.
